Efficiently estimating recall June 09, 2019

If you’re trying to detect or identify an event with a machine learning system, the metrics you really care about are precision and recall: if you think of the problem as finding needles in a haystack, precision tells you how often your system mistakes a straw of hay for a needle, while recall helps you measure how often your system misses needles entirely. Both of these metrics are important in complementary ways. The way I like to think about it is that measuring precision tells you where your model made a mistake while measuring recall tells you where your model can improve.

In most real applications (and in accordance with our haystack metaphor) the positive class we care about tends to be much rarer than the negative class. As a result, recall is quintessentially hard to measure because no one really knows how many needles are in the haystack and there’s too much hay to go through and count it manually. A naive solution is to start counting straws of hay until you have enough samples to get a reasonable estimate of recall (what I’ll call exhaustive or recall-oriented annotation) – however, because there’s an order of magnitude more hay than there are needles so you’ll have to go through a lot of hay to get a good estimate. On the other hand, precision tends to be relatively easy to measure: instead of sifting through the haystack to find needles, you just need to inspect (or have paid annotators inspect) the “needles” predicted by your system and track how many times it got it right or made a mistake (I’ll call this precision-oriented annotation). It can cost roughly cost 10 times as much to annotate for recall as it does to annotate for precision!

Is there a more cost-effective way to measure recall than exhaustive annotation? In this article, I’ll describe a simple but effective technique Ashwin Paranjape and I came up with to leverage relatively cheap precision-oriented annotations to reduce the costs of measuring recall by about a factor of three. This post will stay high-level and focus on the key ideas, but you can find all the gory details and proofs in our EMNLP 2017 paper.

Case study: extracting relational facts from documents

Before we proceed, I’d like to ground the problem into a concrete use-case. The one that I’ve studied most extensively has been that of knowledge base population (KBP) or relation extraction: given a document corpus, we’d like to identify relationships between people and organizations mentioned in the dataset.

Consider the following sentence about the late actress, Carrie Fisher:

[Fisher]’s mother, [Debbie Reynolds], also an [actress], said on Twitter on Sunday that her daughter was stabilizing.

A KBP system must identify that (a) ‘Fisher’ refers to Carrie Fisher, (b) Carrie Fisher and Debbie Reynolds are related by a “parent-child” relationship and (c) that Carrie Fisher was an actress. While this example is relatively simple, there are lots and lots of unique ways in which facts are described in text making this a very challenging task.

Given a corpus of (say) 100,000 news articles, how do we know how much information about Carrie Fisher our system has identified from these articles? How many such bits of information are there even? These are precisely the types of questions measuring recall will help us answer.

Why is estimating recall so hard?

In both the scenarios described above, the key reason that estimating recall is hard is that “you don’t know what you don’t know.” If you want to collect the data needed to measure recall it’s hard to avoid having a person identify needles that the model was not able to. In most practical scenarios, that just requires a substantial amount of effort.

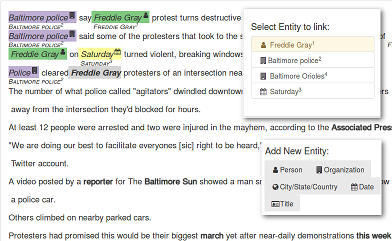
Let’s look at our case study as an example. We spent almost a month of iterating interface designs to help annotators (a) verify the relation between two entities extracted by a system (precision-oriented annotations) and (b) identify all possible relations within a single document (recall-oriented annotations). In order to measure recall, annotators had to first identify all the possible entities in the document and then ascertain if the text described a relationship between any of them (Figure 1). We found that recall-oriented annotation took about ten times longer per fact as compared to precision-oriented data annotation. The actual difference in annotation time (and, as a corollary, cost) will vary by task and interface, but the difference is typically substantial.

Can we use a model to reduce the costs of recall-oriented annotation?

It is tempting to think that we can make this process more efficient by using the model by only showing people things that the model finds “likely”². This mode of annotation looks more similar to what’s needed to measure precision, which we’ve seen can be substantially cheaper³. Unfortunately, this approach can introduce substantial bias in our measurements: we are unlikely to annotate any facts that our model places low probability mass on, and consequently we may never realize that we’ve missed those facts, inflating our estimates of recall.

A popular workaround is to combine the “likely” facts from many different systems with the hope that using the union of their predictions gives us enough coverage to approximate true recall (Figure 2). This measure is called pooled recall and is one of the official evaluation measures used by the TAC-KBP shared task: pooled recall is measured by comparing how many facts a single system found with the union of all the facts found by the teams that participated that year⁴.

However, in our paper we show that there are two key problems with pooled recall:

1. In practice, even the union of 20–30 systems does not provide sufficient coverage to approximate true recall.
2. Naive measurements of pooled recall are biased because of correlations between the systems that are combined.

In essence, naive pooled recall, while significantly cheaper to measure, is a biased approximation of true recall.

In the next two sections, we’ll first show to combine exhaustive annotations with pooled recall to fix the coverage problem and then we’ll provide a new estimator to fix the bias problem. Put together, we’ll have a simple, correct (unbiased) and efficient estimator for recall.

Key idea 1: Use exhaustive annotations to extrapolate the coverage of pooled recall.

As we saw in the previous section pooled recall underestimates true recall because it simply doesn’t cover all the facts in our universe (see Figure 2 for a visual aid). Our fix this problem is very simple: we will extrapolate true recall of a system (\(S_i\)) from its pooled recall by using a separate estimate of the true recall of the pool of systems (\(\bigcup_j S_j\)): \[\text{TrueRecall}(S_i) = \text{TrueRecall}\left( \bigcup_j S_j \right) \times \text{PooledRecall}(S_i).\]

Explained via analogy, suppose we are trying to measure what fraction of PhDs in the world are doing computer science, \(\text{TrueRecall}(\text{CS PhDs})\). For the purposes of this example, let’s assume that every country has an equal distribution of PhDs. The above equation essentially says we can break up our computation into first measuring how many CS PhDs there are in the United States, \(\text{PooledRecall}(\text{US CS PhDs})\), and then multiplying it by the fraction of PhDs from the United States, \(\text{TrueRecall}(\text{US PhDs})\). This roundabout way of measuring \(\text{TrueRecall}\) works if we can measure \(\text{PooledRecall}\) to a greater precision than \(\text{TrueRecall}\), e.g. if the NSF tracks doctorate recipients in the US better than other countries do.

Why does this help us? Intuitively, we’re able to exploit the fact that, for the same cost, we can collect ten times as many precision-oriented annotations to estimate pooled recall and thus significantly reduce the variance of our estimate of pooled recall.

Key idea 2: Use importance sampling to correct bias when estimating pooled recall.

The final problem we’ll need to solve is correcting the bias introduced when naively combining the output from different systems. Figure 3 shows a simple example of how this bias is created: when two systems have correlated output (e.g. they were trained on similar data and hence predict similar relations), sampling independently from each component system will lead to some regions (\(A \cup B\), the dark blue region) being over-represented. As a result, systems that predict more unique or novel relations (e.g. \(C\) in the figure) would measure lower on pooled recall than the other systems (\(A\) and \(B\)) even if they all have the same true recall.⁵

One way to resolve this problem is to sample uniformly from the whole pool instead of sampling each system independently. Unfortunately, this approach doesn’t really let you reuse your annotations when adding new systems into the pool: the distribution from which you sampled output has now changed.

Instead, we propose what we call an importance-reweighted estimator that uses independent per-system samples, but re-weights them for each pooled-recall computation. When evaluating a new system, you can still reuse the old annotations with new weights. The resultant estimator looks like this: \[\text{PooledRecall}(S_i) = \frac{\sum_{j} w_{ij} \sum_{x \in \text{Correct}(S_j)} \mathbb{I}[x \in \text{Correct}(S_i)] {q_i(x)}^{-1}}{\sum_{j} w_{ij} \sum_{x \in \text{Correct}(S_j)} q_i(x)^{-1}},\] where \(w_{ij}\) is an arbitrary weighting factor, \(p_j(x)\) is the probability of drawing a particular instance or relation \(x\) from \(S_j\)’s output, \(q_i(x) = \sum_{j} w_{ij} p_{j}(x)\) and \(\text{Correct}(S_j)\) is shorthand for the correct subset of \(S_j\)’s output. I wish I could provide a simplified, non-mathematical explanation of our importance-reweighted estimator, but the details are quite nuanced and I’ll have to refer you to the paper for a complete explanation.

Concluding notes

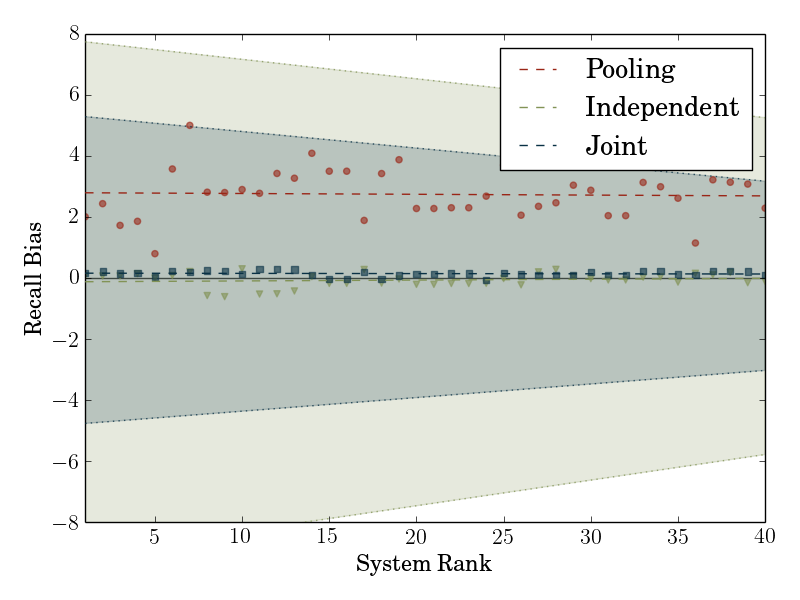
With the two components described above, we finally have an unbiased estimator of true recall that is guaranteed to be more efficient than naive sampling. Figure 4 provides a teaser for how our estimator performs in practice on data obtained through the TAC-KBP shared task. The key takeaways are that a naive pooled estimator is significantly biased, while the importance reweighted estimator presented here has about a third the variance of the naive true recall estimator without introducing any bias.

That’s it for this post: I hope you’ve found at least some of the ideas presented here useful!

Also, many thanks to Aniruddh Raghu and Gabor Angeli for reviewing earlier drafts of this post!

---

1. Note that our measure of intent satisfaction is a bit more nuanced than just call deflection: we want to know how often we’ve helped customers and not just how often we’ve prevented them from talking to a person.↩

2. I put “likely” in quotes because getting meaningful confidence estimates from a statistical model is non-trivial and most of the time the scores returned by the model are quite arbitrary.↩

3. In fact, the annotations collected to measure system precision can be reused to measure pooled recall, which further amortizes the costs of measuring pooled recall.↩

4. As an extra measure to try to reduce the bias of pooled recall, the TAC-KBP organizers also include a human team that tries to identify facts from the corpus within a certain amount of time. Our analysis always incorporates these annotations, and while they help, it’s not by much.↩

5. It’s worth noting that the bias effect described here is an artifact of the sampling process. If one could annotate all of the system’s output, the problem would go away. However, in most real scenarios the system output is large enough that it is impractical if not prohibitively expensive to annotate it all.↩